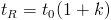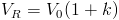Elucja izokratyczna charakteryzuje się stałym, niezmiennym w czasie składem fazy ruchomej, a zatem stałą siłą elucyjną fazy ruchomej. Retencja w tych warunkach jest dana równaniem:
gdzie:- tR – czas retencji
- VR – objętość retencji
- t0 – czas martwy
- V0 – objętość martwa.
Równania te są równoważne wobec V0 = FV0 oraz VR = FtR, gdzie F jest szybkością przepływu fazy ruchomej. Z równań wynika, że objętość retencji, czyli objętość fazy ruchomej, która przepłynęła przez kolumnę do momentu zarejestrowania maksymalnego stężenia związku na wyjściu z kolumny, zależy od objętości martwej, która jest charakterystyczna dla danej kolumny oraz od wartości współczynnika retencji k, który jest charakterystyczny dla danego analitu w danych warunkach analizy. Współczynnik retencji określa podział analitu między fazy:
gdzie:- ns, nm – ilość moli analitu w fazie stacjonarnej (s) i ruchomej (m)
- cs, cm – stężenie analitu w fazie stacjonarnej i ruchomej
- Vs, Vm– objętości fazy stacjonarnej i ruchomej.
W przypadku warunków izokratycznych szerokość piku u podstawy, W, opisana jest zależnością:
gdzie N oznacza liczbę półek teoretycznych i jest miarą sprawności kolumny. Dla danych warunków chromatograficznych N jest traktowane jako stała, jednakowa dla każdego analitu. Z N powiązana jest także wysokość równoważna półce teoretycznej HETP:
gdzie L jest długością kolumny.
Wobec tego, w warunkach izokratycznych szerokość piku u podstawy jest wprost proporcjonalna do czasu retencji analitu. Oznacza to, że im później nastąpi retencja analitu, tym bardziej rozmyty będzie pik.
Literatura
- P. Wiczling, R. Kaliszan: Gradientowa RP HPLC , w: Nowoczesne techniki analityczne, pod red. M. Jarosza, Warszawa : Oficyna Wydawnicza Politechniki Warszawskiej, 2006, s. 67-84.